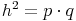Abschnitt: Katheten und Höhensatz | H2MA1/Bürgler/2013

Abschnittsübersicht

In einem rechtwinkligen Dreieck teilt die Höhe hc die Hypotenuse c in 2 Abschnitte.

Diese 2 Abschnitte (p und q) werden als Hypotenusenabschnitte bezeichnet.

$\overline{AH} = q$
$\overline{HB} = p$
$p + q = \overline{AB} = c$

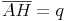
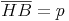
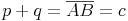Kathetensatz für die Kathete a:

Wenn die beiden Winkel Alpha übereinander liegen und die Seite a auf der Seite c liegt, sieht man, dass sich die beiden Dreiecke ähnlich sind und nur durch ihre Größe unterscheiden.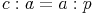

Schreiben wir dieses Verhältnis nun als Bruch an: $\frac{c}{a} = \frac{a}{p}$

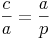
Bringen wir die eine Seite a auf die andere Seite: $\frac{c}{a} = \frac{a}{p}\quad / \quad \cdot a$

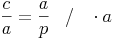
Bringen wir nun die Seite p auf die andere Seite: $c = \frac{a \cdot a}{p}\quad / \quad \cdot p$

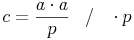
Schreiben wir $a \cdot a$ noch eleganter an: $c \cdot p = a^2$

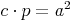
Kathetensatz für die Kathete a:

$a^2 = c \cdot p$

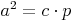Kathetensatz für die Kathete b:

Legt man nun die beiden Dreiecke so übereinander, dass die beiden Winkel Beta übereinander liegen und die Seite b auf der Seite c liegt, so kann man wieder erkennen, dass sich die beiden Dreiecke ähnlich sind und nur durch ihre Größe unterscheiden.

Schreiben wir dieses Verhältnis nun als Bruch an: $\frac{c}{b} = \frac{b}{q}$

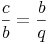
Bringen wir die eine Seite b auf die andere Seite: $\frac{c}{b} = \frac{b}{p}\quad / \quad \cdot b$

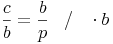
Bringen wir nun die Seite q auf die andere Seite: $c = \frac{b \cdot b}{q}\quad / \quad \cdot q$

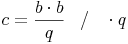
Schreiben wir 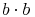$b \cdot b$ noch eleganter an: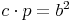 $c \cdot p = b^2$

Kathetensatz für die Kathete b:

$b^2 = c \cdot q$

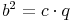Höhensatz:

Das selbe gilt für den Höhensatz. Wenn man die beiden Dreiecke so übereinander legt, dass die beiden Winkel Alpha übereinander liegen und die Höhe hc auf der Seite c liegt, so sieht man wiederum, dass sich die beiden Dreiecke ähnlich sind und nur durch ihre Größe unterscheiden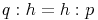

Schreiben wir dieses Verhältnis nun als Bruch an: $\frac{q}{h} = \frac{h}{p}$

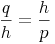
Bringen wir die eine Höhe h auf die andere Seite: $\frac{q}{h} = \frac{h}{p}\quad / \quad \cdot h$

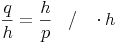
Bringen wir nun die Seite p auf die andere Seite: $q = \frac{h \cdot h}{p}\quad / \quad \cdot p$

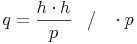
Schreiben wir 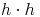$h \cdot h$ noch eleganter an: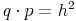 $q \cdot p = h^2$

Höhensatz

$h^2 = p \cdot q$