Abschnittsübersicht

  • Allgemeines

    Alles einklappen Alles aufklappen

  • Satz des Pythagoras

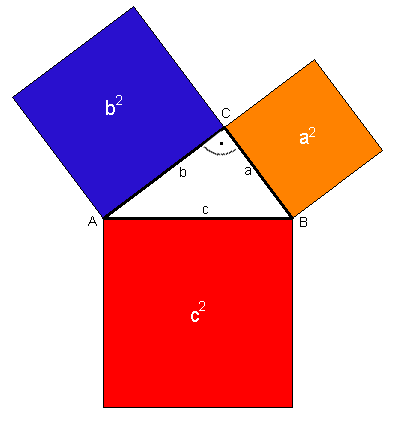
    In jedem rechwinkeligen Dreieck ist die Summe der Flächeninhalte der beiden Kathetenquadrate gleich der Fläche des Hypothenusenquadrats.

    Kurz: Summe der Kathetenquadrate = Hypotenusenquadrat

    a² + b² = c²

    Eigenschaften eines rechtewinkeligen Dreiecks:

    Da ein rechtwinkliges Dreieck einen rechten Winkel (= 90°) hat und die Winkelsumme in jedem Dreieck 180° beträgt, bleibt für die anderen beiden Winkel noch genau 90° übrig.

    Zwei Winkel, die zusammen 90° ergeben, nennt man Komplementärwinkel.

  • Topic 2

    • Teilnehmer/innen müssen
      Als erledigt kennzeichnen

  • Topic 3

    • Teilnehmer/innen müssen
      Als erledigt kennzeichnen

      Das Applet zeigt den Beweis des Euklid für den Satzes von Pythagoras.

      Verändere das rechtwinkelige Dreieck durch das Bewegen der Punkte A und C.

      Bearbeite die folgenden Aufgaben und notiere die Ergebnisse in deinem Heft.
      Verschiebe den Punkt E. Welche Figur entsteht dadurch? Wie groß ist der Flächeninhalt dieser Figur im Vergleich zum blauen Quadrat mit der Seitenlänge b.

      Verschiebe den Punkt E solange in Richtung zum Punkt B, bis bei B ein neuer Punkt F angezeigt wird. Drehe diesen Punkt F auf einem Viertelkreis nach unten.
      Verändert sich dadurch der Flächeninhalt des gedrehten Parallelogramms?

      Verschiebe nun den Punkt G nach unten. Vegleiche das urspüngliche blaue Quadrat mit der Seitenlänge b und das neu entstandene Rechteck. Welchen Flächeninhalt haben sie?

  • Satz des Pythagoras (Mathe-Song)

  • Konstruktion

    KONSTRUKTION EINES RECHTWINKELIGEN DREIECKS

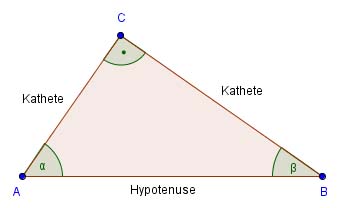
    Hypotenuse

    Als Hypotenuse bezeichnet man die längste Seite eines rechtwinkligen Dreiecks. Sie liegt dem rechten Winkel gegenüber.

    Kathete

    Als Kathete wird jede der beiden kürzeren Seiten in einem rechtwinkligen Dreieck bezeichnet. Die Katheten sind also die beiden Seiten des rechtwinkligen Dreiecks, die den rechten Winkel bilden.

    In Bezug auf einen der beiden spitzen Winkel (in der Skizze \alpha) des Dreiecks unterscheidet man die Ankathete dieses Winkels (die dem Winkel anliegende Kathete) und die Gegenkathete (die dem Winkel gegenüberliegende Kathete).

    Sätze:

    Die Beziehung zwischen den Längen der Katheten und der Hypotenuse beschreibt der Satz des Pythagoras, der auch Hypotenusensatz heißt. (Der Satz lautet: Sind a und b die Seitenlängen der Katheten und ist c die Seitenlänge der Hypotenuse, so gilt die Gleichung a² + b² = c²)

    Anders formuliert besagt der Satz des Pythagoras, dass die Summe der Flächeninhalte der beiden Quadrate über den Katheten gleich dem Flächeninhalt des Quadrats über der Hypotenuse ist. Aus dieser Tatsache folgen der Katheten- und der Höhensatz.

    Der Satz des Thales besagt, dass jedes Dreieck im Halbkreis ein rechtwinkliges Dreieck ist.

    Der Fußpunkt der Höhe teilt die Hypotenuse in zwei Hypotenusenabschnitte. Der Kathetensatz und der Höhensatz machen Aussagen über die Längen dieser Teilstrecken.

    Klicke den Link an und lies dir die verschiedenen Möglichkeiten durch , wie du ein Dreick konstruieren kannst. Konstruiere danach jeweils ein Dreieck und lade dies hoch.

     

  • Katheten und Höhensatz

    In einem rechtwinkligen Dreieck teilt die Höhe hc die Hypotenuse c in 2 Abschnitte.

    Diese 2 Abschnitte (p und q) werden als Hypotenusenabschnitte bezeichnet.

    \overline{AH} = q
    \overline{HB} = p
    p + q = \overline{AB} = c
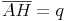
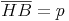
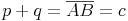    Kathetensatz für die Kathete a:
    Wenn die beiden Winkel Alpha übereinander liegen und die Seite a auf der Seite c liegt, sieht man, dass sich die beiden Dreiecke ähnlich sind und nur durch ihre Größe unterscheiden.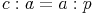
    c : a = a : p

    Schreiben wir dieses Verhältnis nun als Bruch an: \frac{c}{a} = \frac{a}{p}

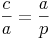
    Bringen wir die eine Seite a auf die andere Seite: \frac{c}{a} = \frac{a}{p}\quad / \quad \cdot a

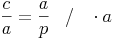
    Bringen wir nun die Seite p auf die andere Seite: c = \frac{a \cdot a}{p}\quad / \quad \cdot p

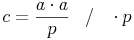
    Schreiben wir a \cdot a noch eleganter an: c \cdot p = a^2

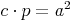
    Kathetensatz für die Kathete a:

    a^2 = c \cdot p
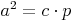    Kathetensatz für die Kathete b:
    Legt man nun die beiden Dreiecke so übereinander, dass die beiden Winkel Beta übereinander liegen und die Seite b auf der Seite c liegt, so kann man wieder erkennen, dass sich die beiden Dreiecke ähnlich sind und nur durch ihre Größe unterscheiden.
    c : b = b : q

    Schreiben wir dieses Verhältnis nun als Bruch an: \frac{c}{b} = \frac{b}{q}

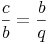
    Bringen wir die eine Seite b auf die andere Seite: \frac{c}{b} = \frac{b}{p}\quad / \quad \cdot b

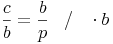
    Bringen wir nun die Seite q auf die andere Seite: c = \frac{b \cdot b}{q}\quad / \quad \cdot q

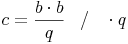
    Schreiben wir 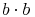b \cdot b noch eleganter an: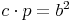 c \cdot p = b^2

    Kathetensatz für die Kathete b:

    b^2 = c \cdot q
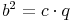    Höhensatz:
    Das selbe gilt für den Höhensatz. Wenn man die beiden Dreiecke so übereinander legt, dass die beiden Winkel Alpha übereinander liegen und die Höhe hc auf der Seite c liegt, so sieht man wiederum, dass sich die beiden Dreiecke ähnlich sind und nur durch ihre Größe unterscheiden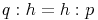
    q : h = h : p

    Schreiben wir dieses Verhältnis nun als Bruch an: \frac{q}{h} = \frac{h}{p}

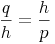
    Bringen wir die eine Höhe h auf die andere Seite: \frac{q}{h} = \frac{h}{p}\quad / \quad \cdot h

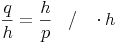
    Bringen wir nun die Seite p auf die andere Seite: q = \frac{h \cdot h}{p}\quad / \quad \cdot p

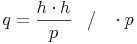
    Schreiben wir 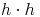h \cdot h noch eleganter an: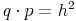 q \cdot p = h^2

    Höhensatz

    h^2 = p \cdot q

  • Satz des Pythagoras - Konstruktion - Sätze

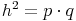
    WIEDERHOLUNG

    Es folgt nun eine Kurzwiederholung. Es handelt sich dabei um fünf Lückentext-Fragen. Die Überprüfung beinhaltet zuvor durgemachte  Theme. 

    Du hast 5 Minuten Zeit um die Antworten zu geben. Lies dir alles gründlich durch und überlege gut bevor du die Antwort gibst.

    • Test
      Teilnehmer/innen müssen
      Als erledigt kennzeichnen

  • Umfang und Flächeninhalt des rechwinkeligen Dreiecks

    UMFANG

    Der Umfang des Dreiecks ergibt sich aus der Summe der drei Seitenlängen

    u = a + b + c

    u = 3 + 4 + 5

    u= 12cm

     

    FLÄCHENINHALT

    Der Flächeninhalt eines rechtwinkligen Dreiecks lässt sich über die Flächeninhaltsformel eines Rechtecks herleiten. Diese lautet ja bekanntlich:

    {A=a{\cdot}b}

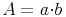
    Fläche = Lange mal Breite

    Zeichnet man die Diagonale des Rechtecks ein, so erhält man zwei deckungsgleiche rechtwinklige Dreiecke.

     

    Der Flächeninhalt eines rechtwinkligen Dreiecks ist halb so groß wie der Flächeninhalt des Rechtecks.

    Die Flächeninhaltsformel des Rechtecks muss also durch 2 dividiert werden.

    Für jedes rechtwinklige Dreieck gilt:

    {A=\frac{a {\cdot} b}{2}}

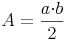
    Flächeninhalt = (Kathete x Kathete) durch 2

    • Formelsammlung Datei PDF
      Teilnehmer/innen müssen
      Als erledigt kennzeichnen

      Hier sind alle Formeln der Ebenen Figuren

      653.8 KB

  • Kurze Überprüfung

    ABSCHLUSSTEST

    Nun ein kurzer Abschlusstest über das gesamte Stoffgebiet. Der Test dauert 10 Minuten. Überlegt euch eure Antworten sorgfältig.

    VIEL GLÜCK

    • Abschlusstest
      Teilnehmer/innen müssen
      Als erledigt kennzeichnen

  • Topic 10